Por Emil Sanchez
O conteúdo deste artigo não necessariamente reflete a opinião da Anicer e é de responsabilidade de seu autor.
Os pilares têm diversas funções na composição estrutural: a) servir de apoio para paredes submetidas às pressões horizontais oriundas da ação do vento; b) resistir às forças verticais provenientes das reações das peças que sobre ele se assentam; c) gerar rigidez nas paredes, conforme ilustrado na Figura 1. Por isso, seu dimensionamento, de acordo com a NBR 16868:2010 ocorre, no caso geral, por flexo-compressão.
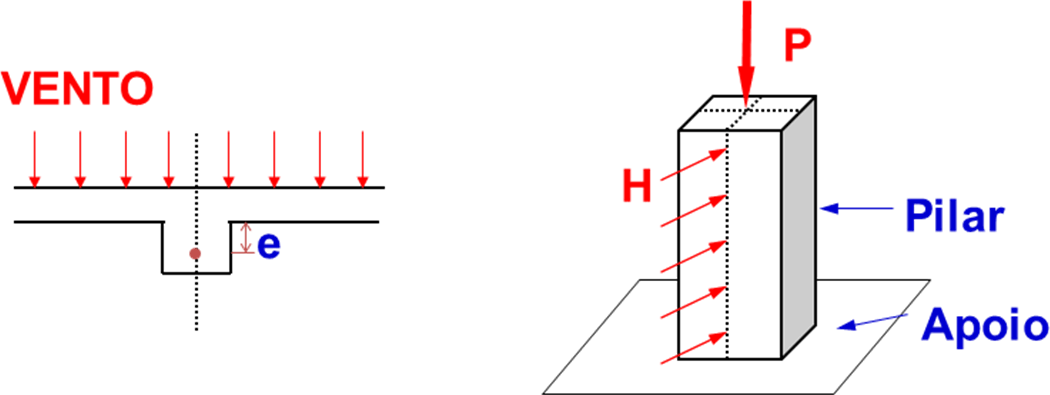
Figura 1
A altura efetiva do pilar será sua altura real quando for considerado bi-rotulado, e duas vezes a altura real no caso de ser engastado na base e livre no topo (Figura 2). A NBR 16868:2010 prescreve as restrições aos deslocamentos para essas condições de contorno.

Figura 2
Na compressão axial, caso muito especial no dimensionamento, na expressão para a força resistente de cálculo se admite um fator R de redução como função apenas do índice de esbelteza da parede, sem a consideração das condições de contorno do pilar, e das excentricidades, originárias de imperfeições executivas e das solicitações a que está submetido. Essa expressão é obtida de forma similar à da parede, mas com uma redução de 10% na força normal resistente de cálculo:
NRd =0,9fd.RA
com o coeficiente redutor que considera somente a esbelteza do pilar
R=1-(λ/40)3
λ=he/te
onde
fd= resistência à compressão de cálculo da alvenaria;
A=área da seção resistente, sem considerar os revestimentos.
A resistência fd, em geral, é obtida ao se considerar a razão básica entre as resistências características do bloco e do prisma preenchido com grout:
fpk /fbk=0,5
A menor dimensão da seção transversal deve ser igual a 14 cm, e se tem para a esbelteza λ os limites de 24 para pilares não armados, e 30 para pilares armados. Ressalta-se que no caso dos pilares não armados toda a seção transversal do pilar deve ser preenchida com grout.
A consideração da esbelteza com uma razão entre a altura efetiva do pilar e sua menor espessura efetiva, λ=he/te, resulta valores inferiores ao se considerar esse parâmetro por meio da expressão clássica da Mecânica dos Sólidos Deformáveis, que é λ=he/i, onde o denominador é o raio de giração da seção transversal. Exemplificando o exposto, para o caso de um pilar isolado com 300 cm de altura, bi-rotulado, dimensões 29 cm X 39 cm ao se empregar os requisitos prescritos na NBR 16868:2010 obtém-se: λ=he/te=300/29=10<16 (pilar curto); entretanto, com a formulação clássica resultará: i=b/3,46=29/3,46=8,4, daí λ=he/i=300/8,4=36. Isto mostra que se fosse um pilar de concreto armado estaria um pouco acima do limite para ser considerado pilar curto.
A menor dimensão da seção transversal deve se 14 cm, e se tem para a esbelteza λ os limites de 24 para pilares não armados, e 30 para pilares armados. Ressalta-se que no caso dos pilares não armados toda a seção transversal do pilar deve ser preenchida com grout.
A consideração da esbelteza com uma razão entre a altura efetiva do pilar e sua menor espessura efetiva, λ=he/te, gera valores inferiores ao se considerar esse parâmetro por meio da expressão clássica da Mecânica dos Sólidos Deformáveis, que é λ=he/i, onde o denominador é o raio de giração da seção transversal. Por exemplo, um pilar isolado com 300 cm de altura, bi-rotulado, com dimensões 29 cm X 39 cm se tem, pela NBR 16868:2010, λ=he/te=300/29=10<16 (pilar curto), mas com a formulação clássica resulta i=b/3,46=29/3,46=8,4, daí λ=he/i=300/8,4=36. Isto mostra que se fosse um pilar de concreto armado estaria um pouco acima do limite para ser considerado pilar curto.
Em seu item 9.3.3 a NBR 16868:2010 prescreve a necessidade de se considerar as excentricidades dos carregamentos sobre os pilares, no caso do dimensionamento à flexo-compressão.
A verificação da resistência do pilar à compressão axial, no Estado Limite Último, é efetuada pela inequação NSd ≤ NRd, onde NSd é a força normal solicitante valor de cálculo.







Deixe um comentário